Quick Sort - 快速排序-数据结构与算法(中)

当前位置:　首页>> 技术小册>> 数据结构与算法(中)

核心：快排是一种采用分治思想的排序算法，大致分为三个步骤。

定基准——首先随机选择一个元素最为基准
划分区——所有比基准小的元素置于基准左侧，比基准大的元素置于右侧
递归调用——递归地调用此切分过程
out-in-place - 非原地快排
容易实现和理解的一个方法是采用递归，使用 Python 的 list comprehension 实现如下所示：
Python:
```asp
 #!/usr/bin/env python

def qsort1(alist):
    print(alist)
    if len(alist) <= 1:
        return alist
    else:
        pivot = alist[0]
        return qsort1([x for x in alist[1:] if x < pivot]) + \
               [pivot] + \
               qsort1([x for x in alist[1:] if x >= pivot])

unsortedArray = [6, 5, 3, 1, 8, 7, 2, 4]
print(qsort1(unsortedArray))
```
输出如下所示：

```asp
[6, 5, 3, 1, 8, 7, 2, 4]
[5, 3, 1, 2, 4]
[3, 1, 2, 4]
[1, 2]
[]
[2]
[4]
[]
[8, 7]
[7]
[]
[1, 2, 3, 4, 5, 6, 7, 8]
```
『递归 + 非原地排序』的实现虽然简单易懂，但是如此一来『快速排序』便不再是最快的通用排序算法了，因为递归调用过程中非原地排序需要生成新数组，空间复杂度颇高。list comprehension 大法虽然好写，但是用在『快速排序』算法上就不是那么可取了。

复杂度分析
在最好情况下，快速排序的基准元素正好是整个数组的中位数，可以近似为二分，那么最好情况下递归的层数为 logn\log nlogn, 咋看一下每一层的元素个数都是 nnn, 那么空间复杂度为 O(n)O(n)O(n) 无疑了，不过这只答对了一半，从结论上来看是对的，但分析方法是错的。

首先来看看什么叫空间复杂度——简单来讲可以认为是程序在运行过程中所占用的存储空间大小。那么对于递归的 out-in-place 调用而言，排除函数调用等栈空间，**最好情况下，每往下递归调用一层，所需要的存储空间是上一层中的一半。完成最底层的调用后即向上返回执行出栈操作，故并不需要保存每层所有元素的值。**所以需要的总的存储空间就是∑i=0n2i=2n\sum _{i=0} ^{} \frac {n}{2^i} = 2n∑i=02in=2n

不是特别理解的可以结合下图的非严格分析和上面 Python 的代码，递归调用的第一层保存8个元素的值，那么第二层调用时实际需要保存的其实仅为4个元素，逐层往下递归，而不是自左向右保存每一层的所有元素。

那么在最坏情况下 out-in-place 需要耗费多少额外空间呢？最坏情况下第 iii 层需要 i−1i - 1i−1 次交换，故总的空间复杂度：

∑i=0n(n−i+1)=O(n2)\sum_{i=0}^n (n-i+1) = O(n^2)∑i=0n(n−i+1)=O(n2)

in-place - 原地快排
one index for partition
先来看一种简单的 in-place 实现，仍然以[6, 5, 3, 1, 8, 7, 2, 4]为例，结合下图进行分析。以下标 lll 和 uuu 表示数组待排序部分的下界(lower bound)和上界(upper bound)，下标 mmm 表示遍历到数组第 iii 个元素时当前 partition 的索引，基准元素为 ttt, 即图中的 target.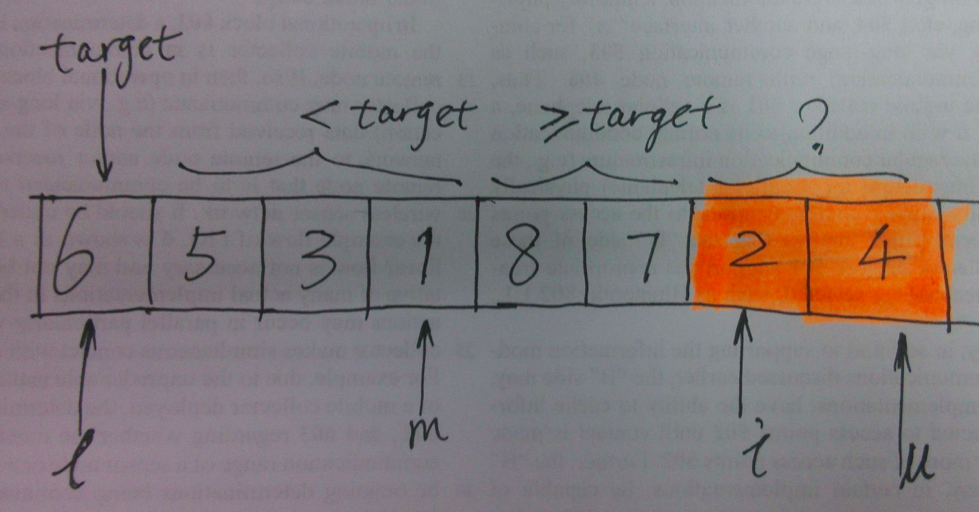

![](/uploads/images/20230407/23f2ba7bff13da4bdd7e50ebb3bb5402.png)

在遍历到第 iii 个元素时，x[i]x[i]x[i] 有两种可能，第一种是 x[i]≥tx[i] \geq tx[i]≥t, iii 自增往后遍历；第二种是 x[i]<tx[i] < tx[i]<t, 此时需要将 x[i]x[i]x[i] 置于前半部分，比较简单的实现为 swap(x[++m], x[i]). 直至 i == u 时划分阶段结束，分两截递归进行快排。既然说到递归，就不得不提递归的终止条件，容易想到递归的终止步为 l >= u, 即索引相等或者交叉时退出。使用 Python 的实现如下所示：

Python
```asp
#!/usr/bin/env python

def qsort2(alist, l, u):
    print(alist)
    if l >= u:
        return

m = l
    for i in xrange(l + 1, u + 1):
        if alist[i] < alist[l]:
            m += 1
            alist[m], alist[i] = alist[i], alist[m]
    # swap between m and l after partition, important!
    alist[m], alist[l] = alist[l], alist[m]
    qsort2(alist, l, m - 1)
    qsort2(alist, m + 1, u)

unsortedArray = [6, 5, 3, 1, 8, 7, 2, 4]
print(qsort2(unsortedArray, 0, len(unsortedArray) - 1))
```

Java
```asp
public class Sort {
    public static void main(String[] args) {
        int unsortedArray[] = new int[]{6, 5, 3, 1, 8, 7, 2, 4};
        quickSort(unsortedArray);
        System.out.println("After sort: ");
        for (int item : unsortedArray) {
            System.out.print(item + " ");
        }
    }

public static void quickSort1(int[] array, int l, int u) {
        for (int item : array) {
            System.out.print(item + " ");
        }
        System.out.println();

if (l >= u) return;
        int m = l;
        for (int i = l + 1; i <= u; i++) {
            if (array[i] < array[l]) {
                m += 1;
                int temp = array[m];
                array[m] = array[i];
                array[i] = temp;
            }
        }
        // swap between array[m] and array[l]
        // put pivot in the mid
        int temp = array[m];
        array[m] = array[l];
        array[l] = temp;

quickSort1(array, l, m - 1);
        quickSort1(array, m + 1, u);
    }

public static void quickSort(int[] array) {
        quickSort1(array, 0, array.length - 1);
    }
}
```
容易出错的地方在于当前 partition 结束时未将 iii 和 mmm 交换。比较alist[i]和alist[l]时只能使用<而不是<=! 因为只有取<才能进入收敛条件，<=则可能会出现死循环，因为在=时第一个元素可能保持不变进而产生死循环。

相应的结果输出为：

[6, 5, 3, 1, 8, 7, 2, 4]
[4, 5, 3, 1, 2, 6, 8, 7]
[2, 3, 1, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 8, 7]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]

该分类下的相关小册推荐：

算法面试通关 50 讲

业务开发实用算法精讲

数据结构与算法(上)

数据结构与算法(下)

编程之道-算法面试(上)

数据结构与算法之美

编程之道-算法面试(下)